Computer Arithmetic

Published on 2022-05-03

Category: Misc

Computer Arithmetic is a broad branch in the fields of Computer Science and Computer Engineering. In this overview, we'll cover essential topics such as binary representation of integers, two's complement encoding, floating-point encoding, and logic gates. While there's much more to computer arithmetic, this post aims to provide a brief introduction to these key concepts.

Binary Representation of Numbers

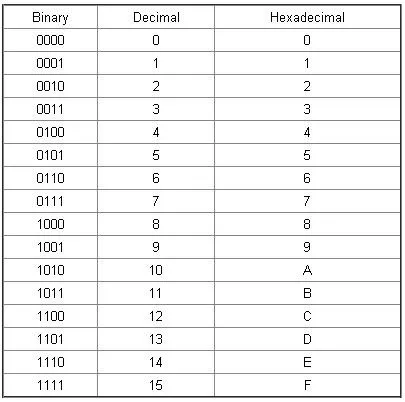
The chart above shows the binary representation of integers from 0 to 15. While hexadecimal values are also important, they won't be covered in this post.

To understand the math behind converting between decimal and binary, I recommend these two YouTube videos by The Organic Chemistry Tutor:

Two’s Complement Encoding

While positive integers are represented straightforwardly in binary, negative integers use two's complement encoding. This method simplifies arithmetic operations, especially addition involving negative numbers. Without two's complement, handling negative numbers would require more complex subtraction operations.

The basic formula for two's complement encoding is:

2^N - x

Where:

x is the absolute value of the negative number
N is the number of bits

Let's take the number -1 as an example, using 5 bits:

2⁵ - 1 = 32 - 1 = 31

Now, convert 31 to binary in 5 bits:

You can apply this method to any negative number with any number of bits using the formula above!

Floating-Point Encoding

Floating-point encoding can seem intimidating, especially when working with scientific notation. Floating-point numbers are typically represented in a 32-bit format divided into three sections:

Sign (1 bit): Indicates if the number is positive (0) or negative (1).
Exponent (8 bits): Encodes the exponent part.
Fraction (23 bits): Encodes the mantissa or fractional part.

Example 1:

Convert the binary scientific notation 1.11111 x 2¹¹¹ to floating-point encoding.

Sign Bit: Since the number is positive, the sign bit is 0.

Exponent:

The exponent in binary is 111, which is 7 in decimal.
Add the bias (127) to the exponent: 7 + 127 = 134.
Convert 134 to binary: 10000110.

Fraction:

Take the fractional part after the binary point: 11111.
Pad it to 23 bits: 11111000000000000000000.

Final Floating-Point Encoding:

Sign:       0
Exponent: 10000110
Fraction: 11111000000000000000000

Floating-Point Encoding Example 1 — Figure: Floating-point encoding of 1.11111 x 2¹¹¹

Example 2:

Convert the binary scientific notation -1.010101 x 2^-0110001 to floating-point encoding.

Sign Bit: Since the number is negative, the sign bit is 1.

Exponent:

The exponent in binary is 0110001, which is 49 in decimal.
Subtract the exponent from the bias: 127 - 49 = 78.
Convert 78 to binary: 01001110.

Fraction:

Take the fractional part: 010101.
Pad it to 23 bits: 01010100000000000000000.

Final Floating-Point Encoding:

Sign:       1
Exponent: 01001110
Fraction: 01010100000000000000000

Floating-Point Encoding Example 2 — Figure: Floating-point encoding of -1.010101 x 2^-0110001

Logic Gates

Logic gates are fundamental building blocks of digital circuits. They are used in transistors, which in turn build processors for CPUs. Logic gates are also essential for constructing functional units.

The four main types of logic gates are:

AND Gate

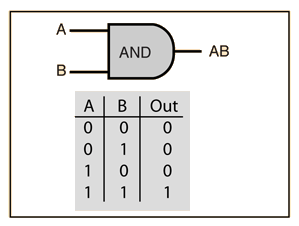
The AND gate outputs 1 only if both inputs are 1.

OR Gate

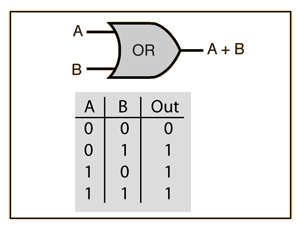
The OR gate outputs 1 if at least one input is 1.

Exclusive OR (XOR) Gate

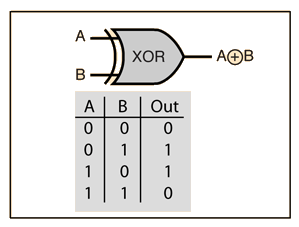
The XOR gate outputs 1 if the inputs are different.

NOT Gate

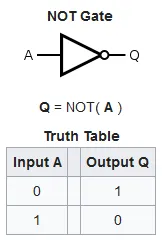
The NOT gate inverts the input signal.

Conclusion

This brief overview covered some fundamental concepts in computer arithmetic, including binary representation, two's complement encoding, floating-point encoding, and logic gates. Understanding these basics is essential for deeper exploration into computer architecture and digital systems.